Gcd Of Two Numbers Using While Loop in CPP

Source Code

#include <iostream>

using namespace std;

int main(int argc, char** argv) {
 

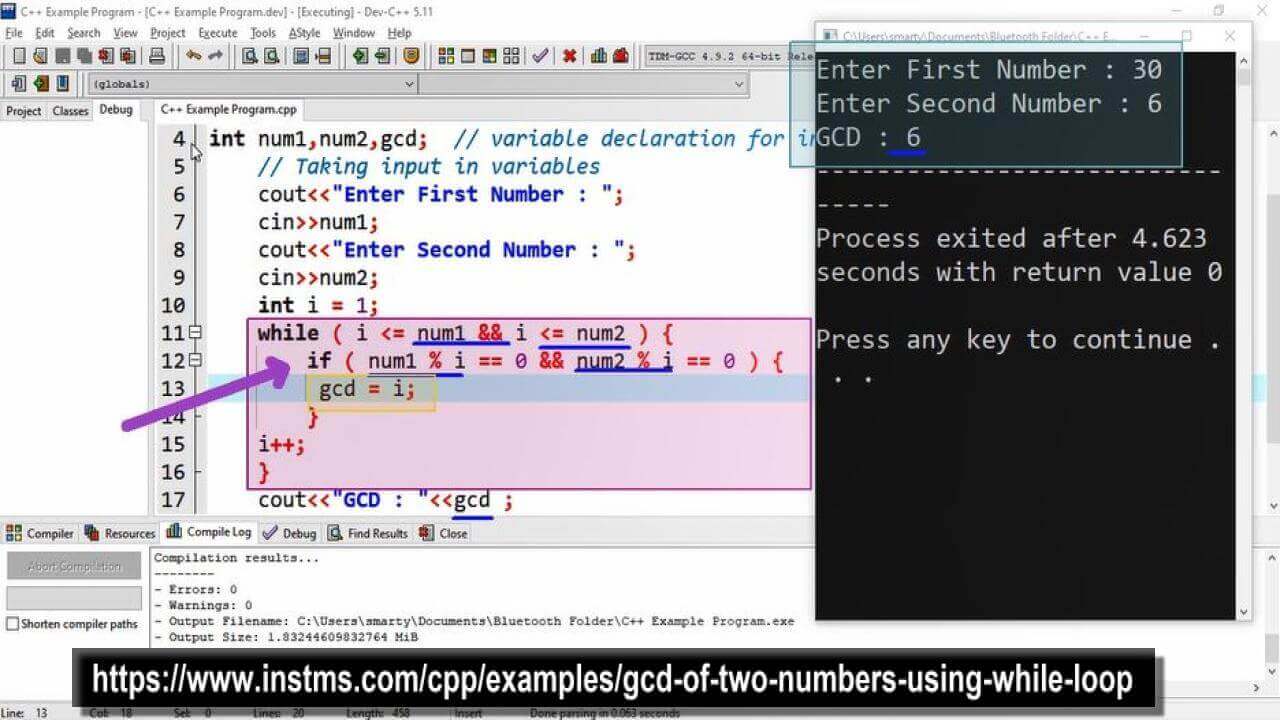
int num1,num2,gcd;  // variable declaration for input
    
    // Taking input in variables
    cout<<"Enter First Number : ";
    cin>>num1;

    cout<<"Enter Second Number : ";
    cin>>num2;

    int i = 1;

    while ( i <= num1 && i <= num2 ) {

    if ( num1 % i == 0 && num2 % i == 0 ) {

     gcd = i;

     }

       i++;

    }
    cout<<"GCD : "<<gcd ;

return 0;
}

Output

Working

GCD stands for Greatest Common Divisor. It will the number which completely divide the given numbers and will be largest. So take the example that if we have two numbers let suppose 30 and 6. Then first of all we have to find the divider of these given numbers. "The divisor of these number are also called factors of given number". Because it completley divide the given number. So as the defination lets start to find the factors of given numbers.

30 = 1, 2, 3, 5, 6, 15, 30

Where  1, 2, 3, 5, 6, 15, 30 are dividors of 30.

6 = 1, 2, 3, 6

Where  1, 2, 3, 6 are dividors of 6

Now from these two list of dividors we have to get greater number, which is 6. So that GCD of 30, 6 will be 6.

Similar implementation is done using C++. Where i which is a counter variable starts from 1. Because we have already know that fators of any number starts from 1. After that in while loop condition we write that loop will run until i will be equal to any one of the given number.

In loop body we put a condition that if any i completely divide the both numbers then it will be the GCD. The loop will repeat its statement and when i completely divide both numbers it will update gcd variable value.

After loop completion we will have GCD in gcd variable. GCD is also called Highest Common Factor, because dividers are factors of the given number.