Selection Sort
Similar to bubble sort algorithm selection sort is also suitable for small data sets. The time complexity increased when the the data set is large. So that selection sort also not commonly preferable. However this sorting technique provide efficient uses of space in contrast of many other sorting algorithms.
Algorithm:
In algorithm Min Pointer is the variable that is used to keep track of sorted and un-sorted list boundries. If we want to sort the data set in Ascending order then we will find/search small values from the un-sorted list repeatedly, otherwise we will find maximum value (In case of Descending Order).
1. Set Min Pointer to 0 index
2. Find minimum/maximum element from Array
3. Swap location Min Pointer with minimum/maximum
4. Increment Min Pointer to point to next element
5. Repeat From 1 Until Array is Sorted
Visual Presentation:
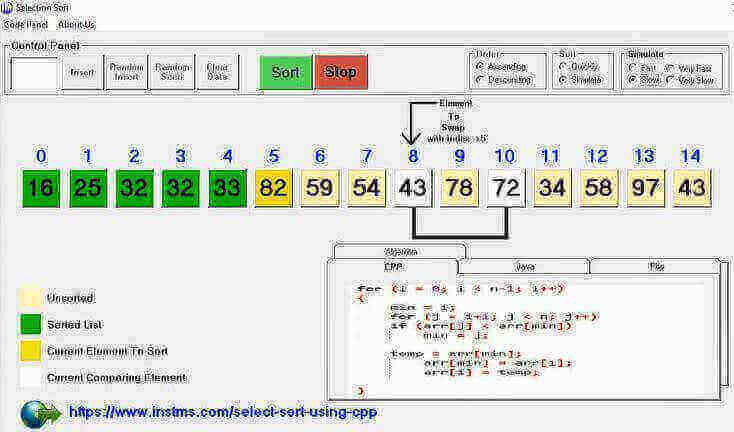
Working:
This algorithm maintain two data sets to process the entire input. This can be observed as sorted and un-sorted list. Initially sorted list will be empty and the un-sorted list will contain the entire values. The boundaries of sorted and un-sorted lists are logically handled by variables. These variables used to store the index values of input array.
Algorithm pick an element from left most of the array and compare it with other elements available in un-sorted list. If this element is greater/small (depending on sorting order) from other elements then it will be the part of sorted list. After placing this element to the right most position of the array (sorted list) the value of variables holding boundaries of sorted and un-sorted list are updated.
This process continue until the entire un-sorted list become sorted list.
Time complexity
| Sr. | Complexity | Worst Case | Average Case | Best Case |
| 1 | Comparisons | O(n)2 | O(n)2 | O(n) |
| 2 | Swaps | O(n) | O(n) | O(1) |
Worst Case:
Advantage of selection sort over bubble sort is that in worst case it required only N swaps to sort out the entire data set.
Average Case:
The time complexity is same in worst as well as in average case. Here it also require N swaps.
Best Case:
In best case of time complexity of both selection sort and bubble sort is similar. There is only one swap required for N comparison.
Selection sort visualization:
Visual basic animation is deveopled by binaryVisual. We can download visual presentation of selection sort algorithm using this link.